Abstract
Physics is a subject that deals with everything that exists, which makes this subject excruciatingly vast and limitless, but what actually makes physics such a huge subject? The answer to this question comes from two areas (i):- quantities and (ii):- processes/procedures the former is discussed in the following article.
It is also quite fascinating that how these two factors establish a connection between physics and everything that exists. In the following article I have tried to explain the relation between physics and every aspect of our life.
The answer to a question

Physics has many definitions about its nature and reaching. One of the many ways to describe the answer to a very simple question that what do we actually study in physics?
The answer to this question is there are two things that we study in physics That are (i):- quantities and (ii):-processes
The processes factor is itself a topic let’s focus ourselves to the physical quantities.
The quantities in physics
In physics we deal with everything around us and everything around us is a quantity/entity. By the variation in the configuration of quantities the physics to study them changes. Everything in existence is made up of quantities whether it is as small as the atom or as big as some galaxy.
These quantities we study in physics are known as Physical Quantities.
Physical quantities are the basic aspects of physics because these are the subject of every experiment, every observation. This will get clearer if we list some of physical quantities e.g. mass, velocity, acceleration momentum etc.
On the basis of the dependence on the change in these quantities with directions these physical quantities are classified into three categories namely (i)- Scalar Quantities, (ii)-Vector Quantities and (iii)-Tensors.
Each type of physical quantity has its own significance in the different areas of physics.
Also, from this topic we the use of mathematics in physics gets increased i.e. this topic introduces many of such topics of mathematics in physics which were never thought to be used in physics before.
- Scalar Quantities

The physical quantities have a nature of having the dependence on the direction or orientation, if their nature doesn’t change due to the change in the direction then these physical quantities are called Scalar Quantities.
To explain more about scalar quantities, consider array of particles shown in figure below, each particle is labeled according to its mass and the coordinate axes shows the orientation of the particles.
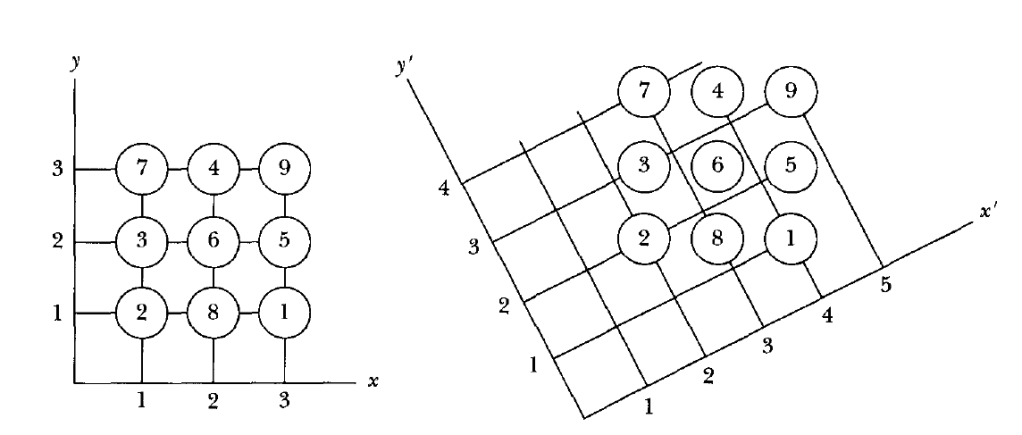
On rotating the axes, we can see the orientation of the particle is changed but the label on the particle i.e. its mass doesn’t change. Hence the label on the particle is an example of the scalar quantities. Here we see that the co-ordinate axes rotation (which symbolizes the change in the direction/orientation of the particle) has no effect on the label of the particle, this accounts the definition of the scalar quantities.
However, you should also notice that there are some factors which do change with the rotation of the axes this represents another type of the physical quantities which are discussed in the next section.
The scalar quantities are generally the most fundamental quantities e.g. mass, length, time, speed, luminous intensity, temperature etc.
The fundamental quantities are the quantities from which all the other quantities are derived and which have a universal value.
2.Vector Quantities

In the illustration given in the previous section, it is clear that the orientation of the particle is changing when the co-ordinate axes were rotated this implies that there are some quantities which have their dependency on the directions.
The quantities that have dependency on both the magnitude as well as direction are known as vector quantities. E.g. velocity, acceleration, momentum etc.
In the above illustration it is clear that the label on the particle is a scalar quantity that doesn’t change with change in the axes(direction) but if we talk about the particle itself it is a vector quantity because its representation depends on both the label and the coordinates i.e. the particle is represented in the way M(x,y) however after axes rotation the “M” remains same but “(x,y)” changes hence the representation of the particle changes.
This accounts for the definition of the vector quantities.
The vector quantities have their own algebra, in which we use several mathematical principles to describe the result of interaction between two or more vectors. Some of the operations are expressed by the equations below.

Vector algebra is foundation for most of the concepts in physics, the best example is the branch of physics called Mechanics, in mechanics we deal with most of the vector quantities such as acceleration, velocity, force momentum etc. the entire mechanics depends on vectors and their operations e.g. we can never apply the 2nd law of motion given by sir Isaac Newton if we us don’t use the vector algebra to calculate the resultant of all the forces acting on the object under observation.
Vector quantities are also the reason of introduction of the new types of the coordinate systems for observing phenomena e.g. we often use the polar coordinate system to observe such motions in which only the direction of motion and the starting point of the object is given.
3.Tensors
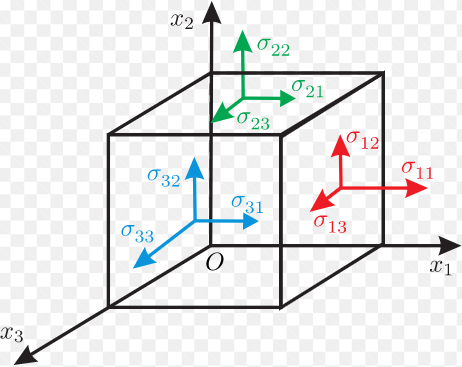
Tensors are general way of defining a physical quantity in the mathematical formulation. In more technical words we can say that it is the super set of the vectors and scalar quantities.
Describing mathematically, tensors are the matrix representations of physical quantities, the rank and the order of these matrices describes the type of physical quantity. Tensors of rank (or order) zero are just scalars and tensors of rank one, are just vectors.
The tensors with a rank higher than one are simply called tensors.
The representation of tensor is done as follows:-
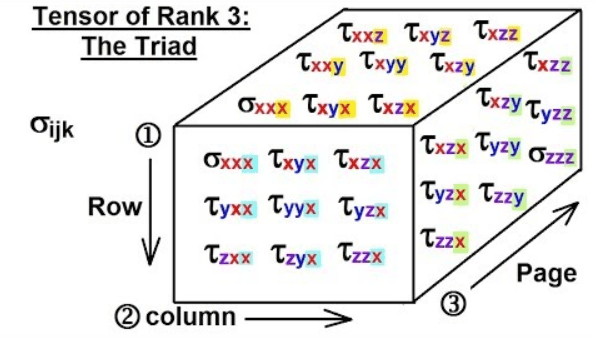
Where the elements of the matrix are the components in different directions depending upon the coordinate system used to describe the quantity.
